|
Цель: получение студентами навыков построения фазовых
портретов двумерных автономных динамических систем и анализа характера
устойчивости точек равновесия системы.
Вариант 13

определим
выражения для правых частей системы уравнений:
> 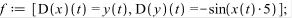

определим начальные условия:
> 

Фазовый портрет(совокупность всех фазовых траекторий
системы) будет иметь вид:

Рис. 1 Фазовый портрет системы 1
Попробуем изменить начальные условия:

Фазовый портрет примет следующий вид:

Рис. 2 Фазовый портрет системы 2
Классификация состояний равновесия динамических систем
второго порядка
Определение правых частей автономной системы:
> 


Определение автономной системы дифференциальных уравнений:
> 

Получение уравнений равновесия (функция subst осуществляет подстановку
новых значений или переменных в указанное выражение):
> 

Поиск координат точек равновесия (функция solve осуществляет поиск
решений заданной системы уравнений относительно заданных переменных, функция
convert преобразует массив выражений в систему уравнений):
> 

Вычисление матрицы линеаризации системы (функция jacobian из пакета
линейной алгебры linalg вычисляет Якобиан векторной функции, в данном случае
матрицу устойчивости для заданной системы):
> 

Вычисление характеристического многочлена (вычисление проведено в
символьном виде):
> 

Вычисление корней характеристического многочлена - собственных чисел
матрицы А в символьном виде:
> 

Выделение из множества равновесий их координаты:
> 

> 





Вычисление собственных чисел матрицы устойчивости для обеих точек
равновесия подстановкой в выражения для собственных чисел - eig_eq - значений
координат точек равновесия (функция simplify обеспечивает максимально возможное
упрощение получаемых выражений):
> 

Построение фазового портрета системы Лотки - Вольтерра:
> 

> 

Рис. 3 Глобальный фазовый портрет системы Лотки -
Вольтерра 1
Корни - чисто мнимые числа. Соответственно состояние
равновесия - центр.
Изменим условие:

> 


Рис. 43 Глобальный фазовый портрет системы Лотки -
Вольтерра 2
динамический система матрица равновесие
На фазовом портрете центр с точкой устойчивости (0;0).
Вывод: получены навыки построения фазовых портретов
двумерных автономных динамических систем и анализа характера устойчивости точек
равновесия системы.
|