|
В традиции некоторых разделов науки зависимость содержания различных ионов (минерализации) от плотности пластовой воды принято представлять в виде
Y = с·(Х-1000), (12)
где X - плотность пластовой воды; Y - степень минерализации; с - некоторый параметр, зависящий от типа растворённых ионов (минералов).
Такой вид зависимости имеет ряд преимуществ по сравнению с традиционным. Во-первых, он обеспечивает нулевое значение степени минерализации для дистиллированной воды, которая имеет плотность, равную 1000, и при этом значении X, и, очевидно, Y равны нулю. Во-вторых, параметр с имеет простой смысл - он показывает, на сколько повышается степень минерализации для пластовой воды, если её плотность возрастает на единицу по сравнению с плотностью дистиллированной воды.
В качестве примера приведём эмпирическую зависимость содержания ионов от плотности воды, поступающей в скважину вместе с нефтью. Для этого был проанализирован состав вод по скважинам горизонта Д1 Ромашкинского месторождения, эксплуатирующимся в течение длительного времени. Для основных ионов пластовой воды: Na+, К+, Сa2+, Mg2+, Cl- - указанная зависимость в пределах изменения плотности пластовых вод 1030-1185 кг/м³ (типичная зависимость) приведена на рис. 2. Очевидно, что она носит линейный характер и хорошо аппроксимируется уравнением
с(ρ) = с · (ρ -1000), (13)
где ρ - плотность воды, поступающей в скважину; с - постоянная величина для данного вида иона, характеризующая концентрацию.

Рис. 2. Зависимости содержания ионов от плотности воды, поступающей в скважину вместе с нефтью
Полученная закономерность подтверждена результатами обработки данных об изменении состава вод при заводнении продуктивных пластов девонского горизонта и верхнего карбона на 121-м месторождении Урало-Поволжья и Западной Сибири.
Чтобы определить коэффициент с в зависимости (12), достаточно сделать замену
= (X - 1000) (14)
Тогда зависимость (12) примет вид
= c·Z (15)
Чтобы найти коэффициент с с помощью МНК, воспользуемся следующими соотношениями. Цель МНК - найти такое значение с, чтобы сумма квадратов отклонений S(c) была минимальной. Сумма квадратов отклонений в данном случае равна
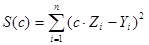
Необходимым условием экстремума является соотношение
 (16) (16)
Соотношение (16) может быть преобразовано к виду:

Отсюда можно определить с:
 (17) (17)
|