|
Истинное значение коэффициента корреляции заключено в пределах
thz1≤ rxixk ≤ thz2, где
z - преобразование Фишера;
th z - гиперболический тангенс аргумента z.
Для определения надежности оценок строится доверительный интервал для полученных оценок в коэффициентов модели:
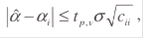
где tp,v - значения критерия Стъюдента с уровнем надежности р и степенями свободы v = (N-n-1),
сii - i-й диагональный элемент матрицы (ХT Х)-1 . Поэтому истинное значение коэффициента a модели будет лежать в интервале
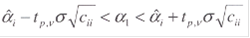
Использование вычислительной процедуры по методу наименьших квадратов с целью получения оценок коэффициентов модели вi, которые удовлетворяли бы условиям несмещенности, состоятельности, эффективности, предполагает выполнение ряда условий:
· независимые переменные представляют собой неслучайный набор чисел, их средние значения и дисперсии конечны;
· случайные ошибки εj - имеют нулевую среднюю и конечную дисперсию
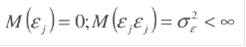
· между независимыми переменными отсутствует корреляция и автокорреляция;
· случайная ошибка не коррелированна с независимыми переменными;
· случайная ошибка подчинена нормальному закону распределения.
Можно выделить условие отсутствия мультиколлениарности, когда несколько независимых переменных связаны между собой линейной зависимостью, и условие гомоскедастичности, т. е. одинаковой дисперсии для всех случайных ошибок. Важным является условие линейной формы связи между зависимой и независимой переменными. Зависимость должна быть именно линейной или сводимой к линейной с помощью некоторых преобразований.
Но иногда исследуемый процесс не может быть сведен к линейной зависимости никакими преобразованиями, как, например, в случае логистической зависимости. Тогда используется ряд методов, например, метод симплексов. Данный метод отличается сравнительной простотой, легкой реализуемостью на ЭВМ, эффективностью при определении оценок коэффициентов модели.
Важной характеристикой реализованной модели является оценка ошибки прогноза:
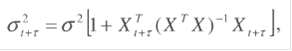
где Хt+τ - вектор значений независимых переменных в момент (t+τ) . Поэтому доверительный интервал для значений зависимой переменной
определяется в момент t как
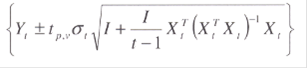
где I - единичный столбец;
tp,v - значение критерия Стьюдента.
Или же находится более эффективная оценка доверительного интервала для прогнозных значений:
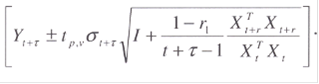
Важным условием получения надежных оценок для модели по методу наименьших квадратов является отсутствие автокорреляции.
Оценка автокорреляции для полученной по МНК модели осуществляется по критерию Дарбина -Уотсона:
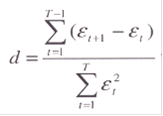
где Т - длина временного ряда.
Полученное расчетное значение d сравнивается с нижней и верхней границей d1 и d2, критерия. Если:
· d < d1, то гипотеза отсутствия автокорреляции отвергается;
· d > d2, то гипотеза отсутствия автокорреляции принимается;
· d1 ≤ d ≤ d2, то необходимо дальнейшее исследование. Одним из известных способов уменьшения автокорреляции является авторегрессионное преобразование для исходной информации или переход к разностям, т. е. ΔYt = Yt+1 -Yt; ΔXt = Xt+1 -Xt.
Если же автокорреляцию устранить не удается, то полученные оценки считаются состоятельными, и среднеквадратическое отклонение корректируется на величину Δj для j-ro коэффициента.
Перейти на страницу: 1 2 3 |