|
2) Рассчитаем вспомогательную величину путем суммирования произведения сумм столбов матрицы на веса альтернатив.
|
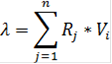
Л1 |
24,9 | |
Л2 |
0,75 | |
Л3 |
0,92 | |
Л4 |
1,9 | |
Л5 |
0,57 | |
Л6 |
1,35 | |
Л7 |
2,45 | |
Л8 |
1,66 | |
Л9 |
6,84 | |
Л10 |
2,6 | |
Л11 |
0,72 | |
Л12 |
2,3 |
) Найдем величину, называемую индексом согласованности.
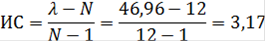
) В зависимости от размерности матрицы парных сравнений находится величина случайной согласованности по таблице 4 (СЛС).
Таблица 4 - Величины случайной согласованности в зависимости от размерности матрицы. |
Размерность матрицы |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 | |
СЛС |
0,58 |
0,9 |
1,12 |
1,24 |
1,32 |
1,41 |
1,45 |
1,49 |
1,63 |
1,92 |
Найдем отношение согласованности.
Если отношение согласованности  , то требуется уточнение матрицы парных сравнений.
Информационный менеджмент и управление процессом производства бытовой химии
Перейти на страницу: 1 2 3 |